データ解析について
相転移(変性・pH滴定)曲線の解析
1.1 二状態転移
反応\(N\rightleftharpoons U\)における平衡定数Kは,各状態のモル分率\(f_{N}\),\(f_{U}\)を用いて,
\[K=\frac{f_{U}}{f_{N}} \tag{1}\]
で与えられる.一方,pH変性においては,変性中点pKaとHill係数νを用いて,
\[K=10^{ν(pH-pK_a)} \tag{2}\]
と表すことができ(ν=1の場合がHenderson-Hasselbalchの式),変性剤による変性の場合は,中点の変性剤濃度C1/2と協同性のパラメータμ,および気体定数Rと絶対温度Tを用いて,
\[K=\exp (\frac{\mu}{RT} (C-C_{1/2})) \tag{3}\]
と表せる(両式は,\(pK_a\to C_{1/2}\),\(2.303\nu\to\frac{\mu}{RT}\)の置き換えにより等価になる.Gibbs自由エネルギー変化\(\Delta G\)に基づく導出はこちら).
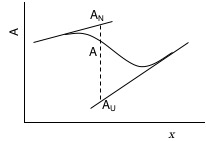
次に,あるpHまたは変性剤濃度(まとめて独立変数xで表す)における観測量Aは,N 状態,U 状態に固有(intrinsic)な観測量AN,AUと,各状態のモル分率fN,fUによって決まり,
\[A=f_N A_N +f_U A_U \tag{4}\]
のように,AN,AUの線形結合として表される.また式(1),(2),(3)より,fN,fUは,C1/2とμ(またはpKaとν)の関数であり,AN,AUは一定の傾きをもつ直線で近似される(右図).
 \[A_N =a_N x +b_N \tag{5.1}\]
\[A_U =a_U x +b_U \tag{5.2}\]
ここでaN,bN,aU,bUは,変性前後のベースラインの傾きと切片である.
\[A_N =a_N x +b_N \tag{5.1}\]
\[A_U =a_U x +b_U \tag{5.2}\]
ここでaN,bN,aU,bUは,変性前後のベースラインの傾きと切片である.
以上をまとめると,あるxiにおける観測量は,
\[A(x_i) =(a_N x_i +b_N)f_N(\mu,c_{1/2})+(a_U x_i +b_U)f_U(\mu,c_{1/2}) \tag{6}\]
で表すことができる.このときの測定値をAobs(xi)とすると,変性(などの相転移)曲線の解析とは,
\[S =\sum_{i=1}^n(A(x_i) - A_{obs}(x_i))^2 \tag{7}\]
を最小にするμ,c1/2,aN,bN,aU,bUを求めることであり(根拠については参考図書1などを参照されたい),これは連立方程式
\[\frac{\partial S}{\partial \mu}=0, \frac{\partial S}{\partial c_{1/2}}=0, \frac{\partial S}{\partial a_N}=0,\frac{\partial S}{\partial b_N}=0, \frac{\partial S}{\partial a_U}=0, \frac{\partial S}{\partial b_U}=0\tag{8}\]
を解くことと同値である.
いま式(6)はaN,bN,aU,bUに関して線形であり,全てのxに関する式全体を
\[\left(\matrix{A(x_1)\cr A(x_2)\cr\vdots\cr A(x_n)}\right)=\left(\matrix{f_N&f_U&f_Nx_1&f_Ux_1\cr f_N&f_U&f_Nx_2&f_Ux_2\cr\vdots&\vdots&\vdots&\vdots\cr f_N&f_U&f_Nx_n&f_Ux_n}\right)\left(\matrix{b_N\cr b_U\cr a_N\cr a_U}\right)\tag{9}\]
のように表すことができる.ここで\(\vec y=\left(\matrix{A(x_1)\cr A(x_2)\cr\vdots\cr A(x_n)}\right)\)はデータベクトル,\(\vec p=\left(\matrix{b_N\cr b_U\cr a_N\cr a_U}\right)\)はパラメータベクトル,\(J =\left(\matrix{f_N&f_U&f_Nx_1&f_Ux_1\cr f_N&f_U&f_Nx_2&f_Ux_2\cr\vdots&\vdots&\vdots&\vdots\cr f_N&f_U&f_Nx_n&f_Ux_n}\right)=\left(\matrix{\frac{\partial A(x_1)}{\partial b_N}&\frac{\partial A(x_1)}{\partial b_U}&\frac{\partial A(x_1)}{\partial a_N}&\frac{\partial A(x_1)}{\partial a_U}\cr \frac{\partial A(x_2)}{\partial b_N}&\frac{\partial A(x_2)}{\partial b_U}&\frac{\partial A(x_2)}{\partial a_N}&\frac{\partial A(x_2)}{\partial a_U}\cr\vdots&\vdots&\vdots&\vdots\cr \frac{\partial A(x_n)}{\partial b_N}&\frac{\partial A(x_n)}{\partial b_U}&\frac{\partial A(x_n)}{\partial a_N}&\frac{\partial A(x_n)}{\partial a_U}}\right)\)はJacobi行列で,式(9)は,
\[\vec y = J\vec p\tag{10}\]
と簡略化して書くことができる(観測方程式).
上式を用いると,(8)の最小2乗化条件は,\(^tJ\)をJの転置行列として,
\[^tJJ\vec p = ^tJ\vec y\tag{11}\]
と表すことができ(正規方程式:導出の詳細は参考図書2または3を参照されたい),
\[\vec p =(^tJJ)^{-1}\ ^tJ\vec y\tag{12}\]
により,各パラメータの最適値を得ることができる.
当研究室が公開しているUnfoldingFitプログラムでは,μとc1/2の初期値を与えて正規方程式(12)を解くことによりaN,bN,aU,bUを求めたうえで,非線形最小2乗法であるsimplex法によりμとc1/2を最適化している.
1.2 二状態転移(重み付き)
\(A(x_1),A(x_2),\cdots ,A(x_n)\)で誤差が異なる場合(例えば,変性剤濃度が高いと一般に測定誤差が大きくなる)は,式(7)でSの評価の際にデータ毎に異なった重み\(w(x_i)\)を付けることで反映させることができる. \[S =\sum_{i=1}^n(A(x_i) - A_{obs}(x_i))^2w(x_i) \tag{13}\] 各データの測定誤差\(\sigma_i\)が異なるときは\(w(x_i)=\frac{1}{\sigma_i ^2}\)で,誤差がない(\(\sigma_i =0\))ときは\(w(x_i)=1\)として計算する.UnfoldingFitプログラムでは,測定誤差に負の値を指定すると,\(w(x_i)=0\)としてデータ\(A(x_i)\)を最小2乗化の際に除外して計算する.
1.3 多状態転移
\(m\)個の変曲点が存在する場合,\(m\)+1状態転移となる(\(m\)≥2).このとき式(4)に準じて, \[A=f_0 A_0+f_1 A_1+\cdots +f_m A_m \tag{14}\] が成立する(各状態を番号付けして添字で表した).各状態のベースラインが直線であるとみなすと,線形パラメータが2(\(m\)+1)個,非線形パラメータが(各変曲点ごとにpKaとνがあるから)2\(m\)個の,計2(2\(m\)+1)個のパラメータの最適化問題となる.
1.4 複数の曲線を同時にフィッティングする場合
同一の変性過程を,複数の観測量で測定する場合(異なる吸光度でモニターしたり,CDと蛍光を組み合わせて測定するなど),複数の変性曲線をいっしょに解析することになる.例えば,観測量AとBを同時に解析する場合は,式(10)におけるデータベクトルとして,\(\vec y =\left(\matrix{A(x_1)\cr A(x_2)\cr\vdots\cr A(x_n)\cr B(x_1)\cr B(x_2)\cr\vdots\cr B(x_n)}\right)\)を用いればよい.一般に,\(m\)個の変曲点が存在する\(l\)個の曲線を同時に解析する際には,線形パラメータが2\(l(m+1)\)個,非線形パラメータが2\(m\)個の,計2\((lm+l+m)\)個のパラメータを,\(ln\)個の測定データを用いて最適化することになる.
1.5 特定のパラメータを初期値に固定したい場合
例えば\(n=10, m=1, l=1\)の場合,データの数10個に対して,パラメータの数は6個あるため,変性曲線の形状によっては全てのパラメータを十分な精度で決められないことがある.あるいは理論上ベースラインが水平になる場合(pH滴定曲線など)には,その傾きを 0(定数)として固定する必要がある.このようなときは,観測方程式(9)の右辺を,対応するパラメータのみ展開して左辺に移項する.例えば,パラメータaU(U 状態のベースラインの傾き)を固定する場合は,観測方程式として式(9)の代りに, \[\left(\matrix{A(x_1)-f_U a_U x_1\cr A(x_2)-f_U a_U x_2\cr\vdots\cr A(x_n)-f_U a_U x_n}\right)=\left(\matrix{f_N&f_U&f_Nx_1\cr f_N&f_U&f_Nx_2\cr\vdots&\vdots&\vdots\cr f_N&f_U&f_Nx_n}\right)\left(\matrix{b_N\cr b_U\cr a_N}\right)\tag{15}\] を用いる.
参考図書
- 小島正樹「薬学のための統計教科書」(東京図書)2015年
- 中川徹・小柳義夫 「最小二乗法による実験データ解析−プログラムSALS」UP応用数学選書 7(東京大学出版会)1982年
- 一瀬正巳「誤差論」(培風館)1953 年
多成分状態の解析
通常のデータ解析において,ある状態の観測量は,その状態に存在する分子や粒子の数(または濃度)に比例することが多い(観測量が吸光度の場合はBeerの法則として知られる).このとき,多成分系の観測量は,式(4)のように構成成分単独の観測量の線形結合で表されることになる.以下の手法は,データ空間を線形空間と見立てたときの「次元」(要するにデータ行列の階数(rank))を独立な成分の数とみなし,各成分単独の観測量とその存在割合(モル分率)を,SVDで得られた基底を用いて再構築するものである.事例としてタンパク質の変性反応を取り上げるが,CD(円偏光二色性)によるタンパク質の二次構造含量の算出については参考図書1を,その他の事例は参考図書2を参照されたい.
2.1 特異値分解(SVD)の原理
例えばSAXSにおいて,各\(q=\frac{4\pi sin\theta}{\lambda}\)値を\(q_1,q_2,\cdots,q_m,\)測定条件で可変にする物理量(pH,変性剤濃度,時刻など)をxで表し,xの各値を\(x_1,x_2,\cdots,x_n\)とすると,散乱強度Iのデータ行列Dは,
\[D=\left(\matrix{I(q_1,x_1)&I(q_1,x_2)&\cdots &I(q_1,x_n)\cr I(q_2,x_1)&I(q_2,x_2)&\cdots &I(q_2,x_n)\cr\vdots&\vdots&&\vdots\cr I(q_m,x_1)&I(q_m,x_2)&\cdots &I(q_m,x_n)}\right)\tag{16}\]
により定義される(CDの場合は,qを波長λに,I をモル楕円率[θ]に置き換えればよい).線形代数の特異値分解(Singular Value Decomposition)の手法により,式(16)は,
\[D=\left(\matrix{U_1(q_1)&U_2(q_1)&\cdots &U_n(q_1)\cr U_1(q_2)&U_2(q_2)&\cdots &U_n(q_2)\cr\vdots&\vdots&&\vdots\cr U_1(q_m)&U_2(q_m)&\cdots &U_n(q_m)}\right)\left(\matrix{s_1&&&O\cr &s_2&&\cr &&\ddots&\cr O&&&s_n}\right)\ ^tV\tag{17}\]
のように3個の行列の積に一意的に分解される(行列\(^tV\)は行列\(V\)の転置行列).ここで右辺の\(\left(\matrix{s_1&&&O\cr &s_2&&\cr &&\ddots&\cr O&&&s_n}\right)\)は正方行列で,その対角成分は特異値(Singular Value)と呼ばれ,通常は\(s_1\geq s_2\geq\cdots\geq s_n\)のように大小順に並んでいる(数学的根拠は参考図書3を、アルゴリズムは参考図書4を参照されたい).
式(16)と(17)の右辺を成分ごとに比較すると,
\[I(q_i,x_k)=\sum_{j=1}^n U_j(q_i)s_j\ ^tV_{jk}=\sum_{j=1}^n U_j(q_i)s_jV_{kj}\tag{18}\]
が成り立つ.
2.2 独立な成分の数の決定(ノイズのない理想的なデータの場合)
もし元のデータ行列DにL 個(\(L\leq n\))の独立な成分が含まれている場合に特異値分解を行うと,式(17)において,
- 基底関数\(U_1,U_2,\cdots,U_L\)がシグナル成分(q 依存性あり)に対応し,\(U_{L+1},U_{L+2},\cdots,U_n\)がノイズ成分(q 依存性なし)に対応する.
- \(s_1,s_2,\cdots,s_L\)が有限の値で,\(s_{L+1}=s_{L+2}=\cdots =s_n=0\)となる.
このとき式(18)は \[I(q_i,x_k)=\sum_{j=1}^L U_j(q_i)s_jV_{kj}=(s_1V_{k1})U_1(q_i)+(s_2V_{k2})U_2(q_i)+\cdots +(s_LV_{kL})U_L(q_i)\tag{19}\] となり,任意の散乱強度は,L 個の基底関数\(U_1,U_2,\cdots,U_L\)の線形結合で表すことができる.
2.3 独立な成分の数の決定(ノイズを含む実際のデータの場合)
実際のデータにはノイズが含まれるので,
- \(U_1,U_2,\cdots,U_n\)のうち,どこまでがシグナル成分で,どこからがノイズ成分か?
- \(s_1,s_2,\cdots,s_n\)のうち,どこまでが有限の値で,どこからが実質上0とみなせるか?
の判断が必要となる.また判断の指標として\(U_1,U_2,\cdots,U_n\)の形状や,\(s_1,s_2,\cdots,s_n\)の値だけでなく, \[\chi^2(L)\buildrel\rm def\over =\sum_{i=1}^m\sum_{k=1}^n(I(q_i,x_k)-\sum_{j=1}^L U_j(q_i)s_jV_{kj})^2\tag{20}\] で定義される値も使用される.式(18)より\(L=n\)のとき上式の右辺は0になるから,\(\chi^2(L)\)は
という目安を表している(完全に再現できた場合は\(\chi^2=0\)).
2.4 データの再構築(reconstruction)
SVDの結果得られた独立な成分の数をL とすると,実測散乱強度\(I(q_i,x_k)\)は,各成分に固有の散乱強度\(I_1(q),I_2(q),\cdots,I_L(q)\)と,\(x_k\)における各成分のモル分率\(f_1(x_k),f_2(x_k),\cdots,f_L(x_k)\)を用いて, \[I(q_i,x_k)=\sum_{j=1}^L f_j(x_k)I_j(q_i)=f_1(x_k)I_1(q_i)+f_2(x_k)I_2(q_i)+\cdots+f_L(x_k)I_L(q_i)\tag{21}\] ここで各成分固有の散乱強度\(I_1(q),I_2(q),\cdots,I_L(q)\)も基底\(U_1(q),U_2(q),\cdots,U_L(q)\)の線形結合で表すことができるから, \[I_j(q_i)=w_{j1}U_1(q_i)+w_{j2}U_2(q_i)+\cdots+w_{jL}U_L(q_i)\tag{22}\] 式(22)を式(21)に代入して, \[I(q_i,x_k)=\left(\sum_{k=1}^L f_k(x_k)w_{j1} \right)U_1(q_i)+\cdots+\left(\sum_{j=1}^L f_j(x_k)w_{jL} \right)U_L(q_i)\tag{23}\] が得られる.式(19)と(23)を比較すると, \[s_1V_{k1}=\sum_{j=1}^L f_j(x_k)w_{j1},\>\cdots,\>s_LV_{kL}=\sum_{j=1}^L f_j(x_k)w_{jL} \tag{24}\] が成り立つ.以降では,\(L=2\)または3の場合について変性反応の平衡論,速度論モデルに対する適用例を示す(各成分を\(N,I,U\)とし,\(K\)を平衡定数,\(k\)を速度定数とする).当研究室が公開しているSVD & Reconstructionプログラムには,以下の1)〜4)の反応スキームに対するReconstructionプログラムを同梱している.
1)\(N \buildrel K\over\rightleftharpoons U\)の場合
式(24)は,\(k=1,2,\cdots,n\)に対して, \[s_1V_{k1}=f_N(pH_k)w_{N1}+f_U(pH_k)w_{U1}\tag{25.1}\] \[s_2V_{k2}=f_N(pH_k)w_{N2}+f_U(pH_k)w_{U2}\tag{25.2}\] と表される(変性剤による変性でも同様).一方,\(f_N+f_U=1\)より\(K=\frac{1-f_N}{f_N}\)だから, \[f_N(pH_k)=\frac{1}{1+K}=\frac{1}{1+10^{\nu(pH_k-pK_a)}},\ f_U(pH_k)=\frac{K}{1+K}=\frac{10^{\nu(pH_k-pK_a)}}{1+10^{\nu(pH_k-pK_a)}}\tag{26}\] 式(25)の左辺はSVDにより得られるので,式(25)と(26)は,\(2n\)個の式から6個のパラメータ(\(w_{N1},w_{U1},w_{N2},w_{U2},\nu,pK_a\))を求める最小2乗法の問題に帰着する.\(w_{N1},w_{U1},w_{N2},w_{U2}\)の値から式(22)より各成分単独の散乱強度が,\(\nu,pK_a\)の値から式(26)より各成分の存在割合が再構築される.
2)\(N \buildrel K_1\over\rightleftharpoons I \buildrel K_2\over\rightleftharpoons\ U\)の場合
式(24)は,\(k=1,2,\cdots,n\)に対して, \[s_1V_{k1}=f_N(pH_k)w_{N1}+f_I(pH_k)w_{I1}+f_U(pH_k)w_{U1}\tag{27.1}\] \[s_2V_{k2}=f_N(pH_k)w_{N2}+f_I(pH_k)w_{I2}+f_U(pH_k)w_{U2}\tag{27.2}\] \[s_3V_{k3}=f_N(pH_k)w_{N3}+f_I(pH_k)w_{I3}+f_U(pH_k)w_{U3}\tag{27.3}\] と表される.一方,\(K_1=\frac{f_I}{f_N},K_2=\frac{f_U}{f_I},f_N+f_I+f_U=1\)より, \[f_N=\frac{1}{1+K_1+K_1K_2},f_I=\frac{K_1}{1+K_1+K_1K_2},f_U=\frac{K_1K_2}{1+K_1+K_1K_2}\tag{28}\] が成り立つ(ただし\(K_1=10^{\nu_1(pH_k-pH_{a1})},K_1=10^{\nu_2(pH_k-pH_{a2})}\)).したがって,\(3n\)個の式から13個のパラメータ(\(w_{N1},w_{I1},w_{U1},w_{N2},w_{I2},w_{U2},w_{N3},w_{I3},w_{U3},\nu_1,pK_{a1},\nu_2,pK_{a2}\))を求める最小2乗法の問題に帰着する.
3)\(N \buildrel k\over\rightarrow U\)の場合
式(24)は,\(j=1,2,\cdots,n\)に対して, \[s_1V_{j1}=f_N(t_j)w_{N1}+f_U(t_j)w_{U1}\tag{29.1}\] \[s_2V_{j2}=f_N(t_j)w_{N2}+f_U(t_j)w_{U2}\tag{29.2}\] と表される.一方,\(\frac{df_N}{dt}=-kf_N\)より, \[f_N(t_j)=f_N^0\exp(-kt_j),\ f_U(t_j)=1-f_N(t_j)\tag{30}\] したがって,\(2n\)個の式から6個のパラメータ(\(w_{N1},w_{U1},w_{N2},w_{U2},k,f_N^0\))を求める最小2乗法の問題に帰着する.
4)\(N \buildrel k_1\over\rightarrow I \buildrel k_2\over\rightarrow U\)の場合
これまでと同様に,\(j=1,2,\cdots,n\)に対して,
\[s_1V_{j1}=f_N(t_j)w_{N1}+f_I(t_j)w_{I1}+f_U(t_j)w_{U1}\tag{31.1}\]
\[s_2V_{j2}=f_N(t_j)w_{N2}+f_I(t_j)w_{I2}+f_U(t_j)w_{U2}\tag{31.2}\]
\[s_3V_{j3}=f_N(t_j)w_{N3}+f_I(t_j)w_{I3}+f_U(t_j)w_{U3}\tag{31.3}\]
が成り立つ.ただし,\(f_N(t_j)=f_N^0\exp(-k_1t_j),f_I(t_j)=f_I^0\exp(-k_2t_j)+\frac{k_1f_N^0}{k_2-k_1}(\exp(-k_1t_j)-\exp(-k_2t_j))\),\(f_U(t_j)=1-f_N(t_j)-f_I(t_j)\)(導出過程はこちら.他の初期条件でも可).
したがって,\(3n\)個の式から13個のパラメータを求める最小2乗法の問題に帰着する.
参考図書
- van Holde, Johnson, Ho(田之倉優・有坂文雄監訳)「物理生化学」(医学出版)2002年
- Methods in Enzymology 210 Numerical Computer Method (1992) Academic Press Inc.
- 柳井晴夫・竹内啓 「射影行列・一般逆行列・特異値分解」UP応用数学選書 10(東京大学出版会)1983年
- Numerical Recipes in FORTRAN 2nd Ed. (1992) Cambridge University Press