直積演算子による多次元NMRの測定原理
1. はじめに
現在の生命科学において核磁気共鳴(NMR)分光法は、生体高分子の立体構造を解明する基礎的手法となっている。分子量1万以上のタンパク質では、同位体標識してCOSY,NOESY,HSQCといった2次元あるいは3次元NMRスペクトルを測定し、解析に供することが多い。ところが、多次元NMRの測定に用いるパルス系列の意味については、深く言及されないのが常である。通常理解されているNMRの測定原理は、外部磁場によりZeeman分裂した核スピンのエネルギー準位間の遷移に基づくものか、あるいは古典的な磁化ベクトルのパルスによる回転とその後の緩和のモデルによるものである。これらの説明方式は、直観的にわかりやすく、また化学シフト、スピン結合、緩和といったNMRの諸概念や1次元のパルスFT(フーリエ変換)NMRの原理を理解する際には有用であるが、2次元以上の複雑なパルス系列に応答するスピン系を正確に記述するには不十分である。一方、量子統計力学の密度行列の概念を用いれば,核スピン系とそのパルスによる応答を完全に記述し得るが,NMRユーザーの直観的理解に乏しい.この融和をはかるため、1980年代に直積演算子(product operator)によるNMR現象一般の定式化が行われた。product operatorとは以降に示すように、各スピン系における密度行列の特別な基底であるが、各基底が古典的磁化ベクトルの状態によく対応付けられており、NMRのユーザーにとって馴染みやすいものとなっている。このproduct operatorにより多次元NMRの測定原理を本ページでわかりやすく解説する。以下では、磁化ベクトルのモデルより容易に導出可能なLarmor歳差運動や、Bloch方程式などのNMRの古典的概念は既知とする(例えば、Becker(斉藤,神藤訳)「高分解能NMR」東京化学同人 (1983)を参照されたい)。
2. 演算子とケット
量子力学においては、観測する系の状態と観測量とが峻別される。これは、不確定性原理により、観測に伴う系の状態の擾乱を無視できないからである。このため、系の状態を状態ベクトル、観測量を演算子で表す。数学的には、前者はケット(縦ベクトル)、後者は行列として表現できる。ケットは\(|a>\)、演算子(行列)は\(A\)等で表す。ケットは通常の縦ベクトルと同様に和とスカラー倍が定義できる。いま状態が\(|a>\)である系に対して\(A\)の観測を行うと、一般に系は\(|a>\)とは別の状態になり、これを\(A(|a>)\)または\(A|a>\)で表す。ただしある特別な状態\(|a'>\)に対しては、
\[ A|a'>=k |a'> \tag{1} \]
のように、元のケットのスカラー倍となる。このようなケット\(|a'>\)を固有ケット、対応する状態を固有状態、スカラー\(k\)を固有値と呼ぶ。
各ケット\(|a>\)に対しては、これと双対関係にあるブラ(横ベクトル)\(< a|\)が対応する。ブラとケットに関しては、以下のような内積および外積が定義される(左辺は右辺の略記法である)。
\[< b | a>=(< b|)\cdot (|a>)\tag{2}\]
\[| b > < a |=(| b>)\cdot (< a |)\tag{3}\]
またケット\(| a>, | c >\) ,ブラ\(< b |\),演算子\(A\)に関して、
\[(| a>< b |)\cdot | c>=| a >\cdot (< b | c>)\tag{4}\]
\[(< b |)\cdot (A| a>)=(< b | A)\cdot (| a>)\tag{5}\]
という結合則が成り立つため、これを各々\(| a >< b | c>,< b | A | a>\) のように略記する。
ブラとケットの代数に関する他の詳細は、J. J. Sakurai「現代の量子力学(上)」吉岡書店 (1989)を参照されたい。
3. スピン1/2の系
以下特に断りのないかぎり核スピン\(\frac{1}{2}\)の系で考える。この系では、固有状態は\(\alpha\)と\(\beta\)の2個あり、対応する固有ケットを各々\(|\alpha >, |\beta >\)で表す。 \(|\alpha >, |\beta >\)は正規直交化されているものとする。すなわち、
\[<\alpha |\alpha >=<\beta |\beta >=1\tag{6}\]
\[<\alpha |\beta >=<\beta |\alpha >=0\tag{7}\]
またスピンの\(z\)成分は観測量であり、これを\(I_z\)で表す.いま系の状態が\(|\alpha>\)のとき、\(I_z\)を観測すると必ず\(\frac{1}{2}\)という値が得られる(\(I_z\)の単位は\(\hbar =\frac{h}{2\pi}\)で表す.但し\(h\)はPlanck定数)。これを次のように表す。
\[I_{z}|\alpha >=\frac{1}{2}|\alpha >\tag{8}\]
同様に、
\[I_{z}|\beta >=-\frac{1}{2}|\beta >\tag{9}\]
一方、系の任意の状態は、固有ケット\(|\alpha >, |\beta >\)の線形結合で表されるが、この状態において\(I_z\)を観測すると、系は\(|\alpha >, |\beta >\)いずれかの状態に跳び移り、必ず\(\frac{1}{2}\)または\(-\frac{1}{2}\)のいずれかを観測値として得ることになる。ただしどちらの状態に跳び移るかを観測前にあらかじめ知ることはできず、その確率と観測量の期待値がわかるだけである。
いま例として,
\[| a >=\frac{1}{\sqrt{2}}|\alpha >+\frac{1}{\sqrt{2}}|\beta >\tag{10}\]
で表される状態\(| a >\)にある系を考える。このとき、観測により系が\(|\alpha >\)に跳び移る確率は\(|< a |\alpha >|^2\)で、\(|\beta >\)に跳び移る確率は\(|< a |\beta >|^2\)で表される。(10)式よりブラ\(< a |\)は、
\[< a |=\frac{1}{\sqrt{2}}<\alpha |+\frac{1}{\sqrt{2}}<\beta |\tag{11}\]
となるから、
\[|< a |\alpha >|^{2}=|\frac{1}{\sqrt{2}}<\alpha |\alpha >+\frac{1}{\sqrt{2}}<\beta |\alpha >|^{2}=\frac{1}{2}\tag{12}\]
となる。ここで式(6),(7)を用いた。同様に\(|< a |\beta >|^{2}=\frac{1}{2}\)。したがって\(I_z\)の期待値\([I_{z}]\)は、
\[[I_{z}]=\frac{1}{2}\times\frac{1}{2}+(-\frac{1}{2})\times\frac{1}{2}=0\tag{13}\]
となり、\(I_z\)の値として、\(\frac{1}{2}\)または\(-\frac{1}{2}\)が等確率で観測されることになる。一般に、期待値\([I_{z}]\)は、
\[[I_{z}]=< a |I_{z}| a >\tag{14}\]
により計算できる。なお、上記のように確率的にはどちらの値も等価であるということと、実際に\(I_z\)を観測すれば必ず\(\frac{1}{2}\)か\(-\frac{1}{2}\)のどちらかになり中間的な値を得ることはない、ということとは十分区別して理解されたい。式(10)の状態は、具体的には核スピンが\(x\)軸方向を向いている状態に対応する。直観的に考えると、このときのスピンの\(z\)成分は\(0\)であるが、実際に観測すると、量子力学から帰結される通り、\(\frac{1}{2}\)か\(-\frac{1}{2}\)のどちらかの値が得られるのである。
4. 演算子の行列表現
任意のケット\(| a >\)は、固有ケット\(|\alpha >, |\beta >\)を基底として用いることにより、
\[| a >=c_{1}|\alpha >+c_{2}|\beta >\tag{15}\]
のように線形結合の形で表すことができる(係数\(c_{1},c_{2}\)は一般に複素数である)。これを、
\[| a >=\left(\matrix{c_{1}\cr c_{2}}\right)\tag{16}\]
と表す(\(c_{1},c_{2}\)を\(|a>\)の成分という)。もし式(6),(7)のように、基底が正規直交化されているときは、
\[c_{1}=<\alpha | a>,\ c_{2}=<\beta | a>\tag{17}\]
である。
いまケット\(| a >\)として、基底\(|\alpha >\)自身を考えると、式(15)は、
\[|\alpha >=1\cdot |\alpha >+0\cdot |\beta >\tag{18}\]
となるから、\(c_{1}=1,\ c_{2}=0\)が得られる。すなわち
\[|\alpha >=\left(\matrix{1\cr 0}\right)\tag{19}\]
同様に、
\[|\beta >=\left(\matrix{0\cr 1}\right)\tag{20}\]
演算子\(I_z\)も、同様にして基底を用いることにより、
\[I_z=\left(\matrix{<\alpha | I_{z}|\alpha >&<\alpha | I_{z}|\beta >\cr <\beta | I_{z}|\alpha >&<\beta | I_{z}|\beta >}\right)\tag{21}\]
と成分表示することができる。この行列の各成分は、式(6),(8)より、例えば
\[<\alpha |I_{z}|\alpha >=\frac{1}{2}<\alpha |\alpha >=\frac{1}{2}\tag{22}\]
となるから、式(21)は結局
\[I_z=\frac{1}{2}\left(\matrix{1&0\cr 0&-1}\right)\tag{23}\]
となる。
以上のように、状態ケットおよび演算子は、適当な基底を定めることにより、成分表示することができる(これは線形代数により保証されるベクトルや行列の一般的性質である。小島「化学・生命科学のための線形代数」東京化学同人 (2012)などの教科書を参照されたい)。このときの基底の選び方は任意であるが、以下では、成分表示の際の基底には必ず固有ケットを用いるものとする。
5. 密度行列
次に複数のスピンから成る系について考える。いま例として、3個のスピンから成る系を考え、このうち2個が状態\(|\beta >\)に、残り1個が状態\(|\alpha >\)にあるものとする。このとき、系全体の状態はどのように記述されるだろうか?これを、例えば
\[\sqrt{\frac{1}{3}}|\alpha >+\sqrt{\frac{2}{3}}|\beta >\tag{24}\]
としてはならない。(24)式の意味するところは,3節で述べたように「観測の結果,状態\(|\alpha >\)をとる確率が\(\frac{1}{3}\)、状態\(|\beta >\)をとる確率が\(\frac{2}{3}\)となる」状態であり、今問題としているような「スピン全体の\(\frac{1}{3}\)が\(|\alpha >\)状態にあり、\(\frac{2}{3}\)が\(|\beta >\)状態にある」状態とは異なるからである。
このため、次式により密度演算子\(\sigma\)を定義する。
\[\sigma = \sum_{i}w_{i}|\phi_{i}><\phi_{i}|\tag{25}\]
\(|\phi_{i}>\)は\(i\)番目のアンサンブルの状態ケット(必ずしも固有ケットであるとは限らない)、\(w_i\)はこのアンサンブルの割合である。上例は、\(|\phi_{1}>=|\alpha >,\ |\phi_{2}>=|\beta >,\ w_{1}>=\frac{1}{3},\ w_{2}>=\frac{2}{3}\)の場合である。\(\sigma\)も、\(|\alpha >, |\beta >\)を基底として成分表示することができる。4節と同様に考えて、対応する行列(密度行列)は、
\[\left(\matrix{\sigma_{\alpha\alpha}&\sigma_{\alpha\beta}\cr \sigma_{\beta\alpha}&\sigma_{\beta\beta}}\right) = \left(\matrix{\sum_{i}w_{i}<\alpha |\phi_{i}><\phi_{i} |\alpha >&\sum_{i}w_{i}<\alpha |\phi_{i}><\phi_{i} |\beta >\cr \sum_{i}w_{i}<\beta |\phi_{i}><\phi_{i} |\alpha >&\sum_{i}w_{i}<\beta |\phi_{i}><\phi_{i} |\beta >}\right)\tag{26}\]
上述の例について具体的に\(\sigma\)を計算すると、例えば\(\sigma_{\alpha\alpha}\)に関しては、
\[\sigma_{\alpha\alpha}=\frac{1}{3}<\alpha |\alpha><\alpha |\alpha >+\frac{2}{3}<\alpha |\beta><\beta |\alpha >=\frac{1}{3}+0=\frac{1}{3}\tag{27}\]
となる。同様にして\(\sigma_{\alpha\beta}=\sigma_{\beta\alpha}=0,\ \sigma_{\beta\beta}=\frac{2}{3}\)となるから、密度行列\(\sigma\)は、結局
\[\sigma=\frac{1}{3}\left(\matrix{1&0\cr 0&2}\right) \tag{28}\]
となる。
密度行列を用いると、系における観測量\(A\)のアンサンブル平均\([A]\)は、
\[[A]=tr(\sigma A)\tag{29}\]
により求めることができる。右辺は行列\(\sigma Α\) の跡(trace)を表す。いまの例について、\(A\)が\(I_z\)の場合に関して値を求めると、式(23),(28)より
\[\sigma I_{z}=\frac{1}{3}\left(\matrix{1&0\cr 0&2}\right)\frac{1}{2}\left(\matrix{1&0\cr 0&-1}\right)=\frac{1}{6}\left(\matrix{1&0\cr 0&-2}\right)\tag{30}\]
となるから、
\[[I_{z}]=tr(\sigma I_{z})=\frac{1}{6}(1-2)=-\frac{1}{6}\tag{31}\]
となる。一方、考えている系は、\(|\alpha >\)状態(固有値\(\frac{1}{2}\))のものが\(\frac{1}{3}\)、\(|\beta >\)状態(固有値\(-\frac{1}{2}\))のものが\(\frac{2}{3}\)存在するから,\(I_z\)のアンサンブル平均は、
\[\frac{1}{2}\times\frac{1}{3}+\left(-\frac{1}{2}\right)\times\frac{2}{3}=-\frac{1}{6}\tag{32}\]
となり、(31)式の右辺の値と確かに一致する。
別の例として、スピン全体の\(\frac{1}{2}\)が\(|\alpha >\)状態に、残り\(\frac{1}{2}\)が式(10)で表される状態にある系を考える(要するに、全体の\(\frac{1}{2}\)が上向き、残り\(\frac{1}{2}\)が横向きにある状態)。この場合は、第1のアンサンブルは先の例と同様に固有状態にあるが、第2のアンサンブルに関してはそうではない。式(26)において、\(|\phi_{1}>=\frac{1}{\sqrt{2}}|\alpha >+\frac{1}{\sqrt{2}}|\beta >,\ \phi_{2}>=|\alpha >,\ w_{1}=w_{2}=\frac{1}{2}\)として、密度行列σを求めると、
\[\sigma =\frac{1}{4}\left(\matrix{3&1\cr 1&1}\right)\tag{33}\]
となり、
\[[I_{z}]=tr(\sigma I_{z})=\frac{1}{4}\tag{34}\]
となる。一方、\(I_z\)の期待値は、第1のアンサンブルに関しては\(\frac{1}{2}\)、第2のアンサンブルに関しては式(13)より0だから、アンサンブル平均は、
\[\frac{1}{2}\times\frac{1}{2}+0\times\frac{1}{2}=\frac{1}{4}\tag{35}\]
となり、式(34)の結果と一致する。
6. 密度行列の基底-直積演算子
上述のように、複数のスピンから成る系の状態は、密度行列により記述される。次に、これら密度行列を基底の線形結合で表すことについて考える(ここでいう基底とは、4節で述べた成分表示の際に定める基底ケットとは概念上異なるものであることに注意されたい。密度演算子空間における基底であるから、当然基底自身も密度演算子である)。
まず、スピン同士の相互作用がない系を考える。この場合の固有ケットは\(|\alpha >\)と\(|\beta >\)の2個であるから、前節で見た通り、密度行列は2行2列となる。したがって4個の線形独立な密度行列を基底として選べば、任意の密度行列はその線形結合で表すことができる。その際に基底となる密度行列は、できるだけ古典的磁化ベクトルモデルに対応して意味付けられるものを選ぶことにする。このような基底の選び方は幾通りかあるが、1つは、
\[I_{x} =\frac{1}{2}\left(\matrix{0&1\cr 1&0}\right),\ I_{y} =\frac{i}{2}\left(\matrix{0&-1\cr 1&0}\right),\ I_{z} =\frac{1}{2}\left(\matrix{1&0\cr 0&-1}\right),\ \frac{E}{2} =\frac{1}{2}\left(\matrix{1&0\cr 0&1}\right)\tag{36}\]
である。\(I_{x},\ I_{y},\ I_{z}\)は各々古典的磁化ベクトルが\(x\)軸、\(y\)軸、\(z\)軸上にある状態と対応付けられる(\(i\)は虚数単位、\(E\)は単位行列である)。また、他の選び方としては、
\[I^{+} =\left(\matrix{0&1\cr 0&0}\right),\ I^{-} =\left(\matrix{0&0\cr 1&0}\right),\ I_{\alpha} =\left(\matrix{1&0\cr 0&0}\right),\ I_{\beta} =\left(\matrix{0&0\cr 0&1}\right)\tag{37}\]
が考えられる。\(I^{+},\ I^{-}\)は\(I_{x},\ I_{y}\)と
\[I^{+}=I_{x}+iI_{y},\ I^{-}=I_{x}-iI_{y}\tag{38}\]
の関係があり、\(I_{\alpha},\ I_{\beta}\)は\(I_{z},\ E\)と
\[I_{\alpha}=\frac{1}{2}(E+2I_{z}),\ I_{\beta}=\frac{1}{2}(E-2I_{z})\tag{39}\]
の関係がある。また、式(19),(20),(37)より
\[I^{+}|\beta > = |\alpha >,\ I^{+}|\alpha > = 0\tag{40}\]
だから、\(I^{+}\)は系のスピン固有値(磁気量子数)を、\(-\frac{1}{2}\)から\(\frac{1}{2}\)へ増す働きがあり、上昇演算子と呼ばれる.同様に、\(I^{-}\)は下降演算子と呼ばれる(両方あわせて昇降演算子と呼ぶ)。ただし上昇、下降はスピン固有値に対してなされるもので、エネルギーダイアグラム上では上下が逆向きになることに注意されたい。一方、\(I_{\alpha},\ I_{\beta}\)は、スピン\(I\)が各々\(\alpha\)状態、\(\beta\)状態に存在する状態に対応し、分極演算子と呼ばれる。
次に2スピン系(スピン\(I\)と\(S\)とが相互作用している系)について考える。この場合、系の固有ケットは、\(|\alpha\alpha>,\ |\alpha\beta>,\ |\beta\alpha>,\ |\beta\beta>\)の4個であり、密度行列は4行4列となる。したがってその基底として16個の密度行列が必要となるが、これを先程の(36)式の基底(0スピンおよび1スピンに対応)から直積(テンソル積)の演算により作成する(これが直積演算子の名の由来である)。例えば
\[I_{z} =I_{z}E_{s}=\frac{1}{2}\left(\matrix{1&0\cr 0&-1}\right)\otimes\left(\matrix{1&0\cr 0&1}\right)=\frac{1}{2}\left(\matrix{1&0&0&0\cr 0&1&0&0\cr 0&0&-1&0\cr 0&0&0&-1}\right)\tag{41}\]
\[2I_{y}S_{z} =2\frac{i}{2}\left(\matrix{0&-1\cr 1&0}\right)\otimes\frac{1}{2}\left(\matrix{1&0\cr 0&-1}\right)=\frac{i}{2}\left(\matrix{0&0&-1&0\cr 0&0&0&1\cr 1&0&0&0\cr 0&-1&0&0}\right)\tag{42}\]
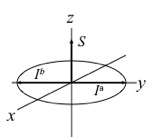
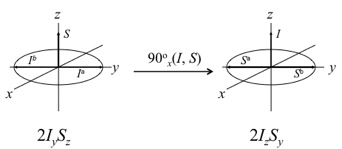
となる。\(I_{z}\)は1スピン系のときと同様、古典的磁化ベクトルモデルにおいて、スピン\(I\)の磁化が\(z\)軸上にある状態と対応付けられる。\(2I_{y}S_{z}\)は反位相(anti-phase)の演算子と呼ばれ、その幾何学的内容は以下の通りである。まず式(39)より
\[2I_{y}S_{z} =I_{y}S_{\alpha}-I_{y}S_{\beta}\tag{43}\]
と変形でき、これは下図のように「\(\alpha\)状態のスピン\(S\)と結合しているスピン\(I\)(\(I^{\alpha}\)で表す)が\(y\)方向を向き、\(\beta\)状態のスピン\(S\)と結合しているスピン\(I\)(\(I^{\beta}\)で表す)が\(-y\)方向を向いている」と考えることができる。結合相手のスピン\(S\)の状態の違いにより、位相が180\(^\circ\)ずれているのが「反位相」の意味である。
他も含めて、基底となる16個を全て挙げると、
\[\frac{1}{2}E,\ I_{x},\ I_{y},\ I_{z},\ S_{x},\ S_{y},\ S_{z},\ I_{z}S_{z}\]
\[2I_{x}S_{z},\ 2I_{y}S_{z},\ 2I_{z}S_{x},\ 2I_{z}S_{y}\]
\[2I_{x}S_{x},\ 2I_{y}S_{y},\ 2I_{x}S_{y},\ 2I_{y}S_{x}\]
となる。中段の4個が反位相の演算子であり、下段4個は2量子遷移、零量子遷移に対応する。以上のように、これらの演算子(直積演算子と呼ぶ)は、古典的磁化ベクトルの動きと対応付けることができ、直観的なイメージが得られやすい。これらを基底として線形結合することにより、初めて系の任意の密度行列が得られるのであるが、実際には、個々の基底の時間発展のみ考慮すれば事足りることを次節以降で示す。
3スピン系では、固有ケットは8個あり、基底として64個の演算子が必要となるが、詳述は避ける。
なお式(19),(20),(36)より、\(I_{x},\ I_{y},\ I_{z}\)の間には
\[\frac{i}{2}I_{x}=I_{y}I_{z},\ \frac{i}{2}I_{z}=I_{x}I_{y},\ \frac{i}{2}I_{y}=I_{z}I_{x},\ \frac{1}{2}E=I_{x}I_{x}=I_{y}I_{y}=I_{z}I_{z}\tag{44}\]
の関係があるが、\(2iI_{x}\)を\(i\)、\(2iI_{y}\)を\(j\)、\(2iI_{z}\)を\(k\)、\(E\)を1とみなせば、四元数(quaternion)の基底の変換則
\[ij=k,\ jk=i,\ ki=j,\ i^{2}=j^{2}=k^{2}=-1\]
と同一である。
7. 密度行列の時間発展
系の密度行列が時間とともにどのように変化するかは、次式のLiouville-von Neumann方程式により規定される。
\[\frac{d}{dt}\sigma (t)=-i[H(t),\sigma (t)]\tag{45}\]
ただし\(\sigma (t),\ H(t)\)は、時刻\(t\)における系の密度行列とハミルトニアンで、右辺の\([H(t),\ \sigma (t)]\)は、交換関係\(H(t)\sigma (t) – \sigma (t)H(t)\)を表す。上式は、Schrödinger方程式と等価であるが、密度演算子を陽に含んでいるため、今の問題には適している。
式(45)は一般的に解くことができるが、これをNMRのスピン系の場合に適用するにあたっては、以下の点が本質的である。
(i) 自由歳差運動におけるハミルトニアン(化学シフトとスピン結合)は時間に依存しないため、式(45)の解は、初期時刻における密度演算子と、回転演算子を用いてより簡単に表される。また、強いラジオ波パルスも回転演算子に対応する。したがって本来多次元空間(2スピン系ならば16次元)の運動である密度演算子の時間発展が、部分空間の2次元的回転運動に還元できる。
(ii) 初期状態である熱平衡状態における系の密度演算子は、直積演算子そのものである(すぐ後で示す)。したがって、まずは直積演算子に関して、(45)式を用いてその時間発展を解けばよい。
(iii) ところが後で示すように、直積演算子の回転の結果は,自身および他のもう1つの直積演算子の線形結合となる。したがって(45)式においては、一般的な密度行列の変換を考える代わりに、始終、その基底である直積演算子の変換だけを考えていればよい。
(iv) 弱い結合によるスピン系の場合(TOCSYの場合を除いて通常は成り立つ)には、ハミルトニアンの化学シフト項とスピン結合項は交換可能なため、密度行列の展開を考える際には、各項の効果を分けて、順次変換を適用すればよい。言い換えれば、パルス,化学シフト,スピン結合による各直積演算子の変換を一度公式としてまとめておけば、任意のパルス系列に対し、首尾一貫した方法で変換を行うことができる。
以降でさらに詳細な説明と補足を行う。
まず(ii)に関しては、熱平衡状態における密度行列\(\sigma (0)\)は、非対角成分が0で、対角成分は各固有状態の割合となる。したがって例えば2スピン系の場合
\[\sigma (0) =\frac{1}{Z}\left(\matrix{\exp\left(\frac{-E_{\alpha\alpha}}{kT}\right)&0&0&0\cr 0&\exp\left(\frac{-E_{\alpha\beta}}{kT}\right)&0&0\cr 0&0&\exp\left(\frac{-E_{\beta\alpha}}{kT}\right)&0 \cr 0&0&0&\exp\left(\frac{-E_{\beta\beta}}{kT}\right)}\right)\tag{46}\]
となる。ここで、\(Z\)は系の分配関数で
\[Z =\exp\left(\frac{-E_{\alpha\alpha}}{kT}\right)+\exp\left(\frac{-E_{\alpha\beta}}{kT}\right)+\exp\left(\frac{-E_{\beta\alpha}}{kT}\right)+\exp\left(\frac{-E_{\beta\beta}}{kT}\right)\tag{47}\]
であり、\(k\)はBoltzmann定数、\(T\)は系の温度である。スピン系の場合、各固有状態のエネルギー\(E\)は,\(kT\)と比べて非常に小さく、\(\frac{E}{kT}\ll 1\)が成り立つので、
\[\exp\left(\frac{-E}{kT}\right)\sim 1-\frac{E}{kT}\tag{48}\]
により近似し、
\[E_{\alpha\alpha}=-\frac{1}{2}(\omega_{I}\hbar +\omega_{S}\hbar),\ E_{\alpha\beta}=-\frac{1}{2}(\omega_{I}\hbar -\omega_{S}\hbar),\]
\[E_{\beta\alpha}=\frac{1}{2}(\omega_{I}\hbar -\omega_{S}\hbar),\ E_{\beta\beta}=\frac{1}{2}(\omega_{I}\hbar +\omega_{S}\hbar)\]
の関係(\(\omega_{Ι},\ \omega_{S}\)は各々スピン\(I,\ S\)のLarmor角周波数(単位はrad/sec))を用いると、\(Z\simeq 4\)となるから
\[\sigma (0)=\frac{1}{4}\left\{\left(\matrix{1&0&0&0\cr 0&1&0&0\cr 0&0&1&0 \cr 0&0&0&1}\right)-\frac{\hbar}{2kT}\left(\matrix{-\omega_{I}-\omega_{S}&0&0&0\cr 0&-\omega_{I}+\omega_{S}&0&0\cr 0&0&\omega_{I}-\omega_{S}&0 \cr 0&0&0&\omega_{I}+\omega_{S}}\right)\right\}\]
\[=\frac{1}{4}\left\{E+\frac{\hbar\omega_{I}}{kT}\left(\matrix{1&0&0&0\cr 0&1&0&0\cr 0&0&-1&0 \cr 0&0&0&-1}\right)-\frac{\hbar\omega_{S}}{2kT}\left(\matrix{1&0&0&0\cr 0&-1&0&0\cr 0&0&1&0 \cr 0&0&0&-1}\right)\right\}\tag{49}\]
となり、式(41)を参照すると、結局
\[\sigma (0)=\frac{1}{4}E+\frac{p_{I}}{4}I_{z}+\frac{p_{S}}{4}S_{z}\tag{50}\]
で表される(\(p_{I}=\frac{\omega_{I}\hbar}{kT},\ p_{S}=\frac{\omega_{s}\hbar}{kT}\))。ここで、単位行列\(E\)は観測量に寄与しないから、(また係数部分\(\frac{p}{4}\)も除いて)通常
\[\sigma (0)=I_{z}+S_{z}\tag{51}\]
と表すことができ、密度演算子は、各スピンの直積演算子そのものとなる。これは古典的ベクトルモデルとも対応している(スピン\(I\)、スピン\(S\)の磁化ともに\(z\)軸方向を向いている状態)。
次に、スピン系のハミルトニアンについて考える。2スピン系の場合、これは
\[H=\omega_{I}I_{z}+\omega_{S}S_{z}+2\pi J(I_{x}S_{x}+I_{y}S_{y}+I_{z}S_{z})\tag{52}\]
と表せる(\(J\)は\(I\)と\(S\)のスピン結合定数)。右辺の前2項は化学シフト項で、残りがスピン結合項である。弱く結合したスピン系の場合、スピン結合項は\(2\pi JI_{z}S_{z}\)のみとなり、(iv)で述べた通り、化学シフト項と交換可能になる。したがって(45)式を解く際、両項を別々に考えればよい。まず化学シフトによる展開であるが、例えば、直積演算子\(I_{x}\)の場合には、式(45)より
\[\frac{d}{dt}I_{x}=-i[\omega_{I}I_{z},\ I_{x}]\tag{53}\]
となる。右辺は、(44)式より\([\omega_{I}I_{z},\ I_{x}] = \omega_{Ι}(I_{z}I_{x} – I_{x}I_{z}) = \omega_{I}iI_{y}\)となるから、結局
\[\frac{d}{dt}I_{x}=\omega_{I}I_{y}\tag{54}\]
同様にして、
\[\frac{d}{dt}I_{y}=-\omega_{I}I_{x}\tag{55}\]
\(I_{x},\ I_{y}\)に関する式(54),(55)の連立微分方程式は、\(I_{z}\)軸周りの回転を表す(\(I_{x},\ I_{y}\)をBloch方程式における磁化ベクトル成分\(M_{x},\ M_{y}\)に置き換えてみればよい)。したがって\(I_{x},\ I_{y}\)平面上において、時間\(\tau\)の間に
\[I_{x}=1I_{x}+0I_{y}=\left(\matrix{1\cr 0}\right)\to\left(\matrix{\cos\omega_{I}\tau\cr \sin\omega_{I}\tau}\right)=(\cos\omega_{I}\tau)I_{x}+(\sin\omega_{I}\tau)I_{y}\tag{56}\]
と変換される。これを
\[I_{x}\buildrel\omega_{I}I_{z}\over\longrightarrow I_{x}\cos\omega_{I}\tau +I_{y}\sin\omega_{I}\tau\tag{57}\]
と表す。同様に、
\[I_{y}\buildrel\omega_{I}I_{z}\over\longrightarrow I_{y}\cos\omega_{I}\tau -I_{x}\sin\omega_{I}\tau\tag{58}\]
式(57),(58)が\(I_{x},\ I_{y}\)の化学シフトによる変換式である。各式の左辺をeductという。直積演算子は変換により、educt自身と、もう1つ別の直積演算子(これをproductという)との線形結合になる。その理由は、上の(i)で述べたように、元来16次元空間における運動(したがって本来ならば右辺は基底である16個の直積演算子全ての線形結合になるはず)が、\(I_{x},\ I_{y}\)平面内における\(I_{z}\)軸まわりの回転に還元できるからである。ゆえに右辺において必ずeductの係数はcosに、productの係数はsinになる。このことは上例に限らず、全ての直積演算子の全ての変換にあてはまる。これが(iii)で述べた事柄である。
次に、スピン結合による変換を考える。式(45)において、\(\sigma =I_{x},\ H = 2\pi JI_{z}S_{z}\)とすると
\[\frac{d}{dt}I_{x}=-i[2\pi JI_{z}S_{z},I_{x}]\tag{59}\]
右辺は計算により\(2\pi JiI_{y}S_{z}\)となるから、先程の\(I_{y}\)の代わりに,今度は\(2I_{y}S_{z}\)(これは6節で述べた反位相演算子である)についてその時間発展を求めてみる。式(45)を用いて
\[\frac{d}{dt}(2I_{y}S_{z})=-i[2\pi JI_{z}S_{z},2I_{y}S_{z}]\tag{60}\]
右辺は\(–\pi JiI_{x}\)だから、式(59),(60)は結局
\[\frac{d}{dt}I_{x}=\pi J2I_{y}S_{z},\ \frac{d}{dt}(2I_{y}S_{z})=-\pi JI_{x}\tag{61}\]
となり、直積演算子\(I_{x},\ 2I_{y}S_{z}\)のスピン結合による変換は、\(I_{x},2I_{y}S_{z}\)平面内の回転となる(そして\(2I_{z}S_{z}\)軸まわりの回転である).これを化学シフトの場合と同様に
\[I_{x}\buildrel 2\pi JI_{z}S_{z}\over\longrightarrow I_{x}\cos\pi J\tau +2I_{y}S_{z}\sin\pi J\tau\tag{62}\]
\[2I_{y}S_{z}\buildrel 2\pi JI_{z}S_{z}\over\longrightarrow 2I_{y}S_{z}\cos\pi J\tau -2I_{x}\sin\pi J\tau\tag{63}\]
と表す。スピン結合の場合は横磁化(\(I_{x}\)または\(I_{y}\))の変換により、反位相演算子がproductとして現れること、また反位相磁化の展開により再び横磁化(「同位相の横磁化」とも呼ばれる)が現れることが重要である。
通常、\(t_{1}\)期、\(t_{2}\)期の自由歳差運動では、化学シフトとスピン結合による展開が同時に起こるが、両ハミルトニアンが交換可能なため、上の(iv)により、変換は順次別々に行えばよい。例えば、\(I_{x}\)の場合には
\[I_{x}\buildrel\omega_{I}I_{z}\over\longrightarrow I_{x}\cos\omega_{I}\tau +I_{y}\sin\omega_{I}\tau\]
\[\buildrel 2\pi JI_{z}S_{z}\over\longrightarrow I_{x}\cos\omega_{I}\tau\cos\pi J\tau +2I_{y}S_{z}\cos\omega_{I}\tau\sin\pi J\tau\]
\[+I_{y}\sin\omega_{I}\tau\cos\pi J\tau - 2I_{x}S_{z}\sin\omega_{I}\tau\sin\pi J\tau\tag{64}\]
となる。
最後に、ラジオ波パルスによる変換を考える。パルスの場合は、古典的磁化ベクトルモデルと同様、パルスをかける軸まわりの回転としてとらえればよい(ただし直積演算子では座標系は右手系である)。
\[I_{z}\buildrel\frac{\pi}{2}I_{x}\over\longrightarrow -I_{y},\ I_{y}\buildrel\frac{\pi}{2}I_{x}\over\longrightarrow I_{z}\tag{65}\]
また\(2I_{y}S_{z}\)などでは、\(I\)と\(S\)を別々に取り扱えばよく
\[2I_{y}S_{z}\buildrel\frac{\pi}{2}(I_{x}+S_{x})\over\longrightarrow -2I_{z}S_{y}\tag{66}\]
これは、\(S\)に関する反位相の磁化成分\(I_{y}\)が、\(I\)に関する反位相の磁化成分\(S_{y}\)に変換したことを表し、後述する分極移動の現象の基礎になっている。
他の直積演算子の変換式は、成書に載っているので、そちらを参照されたい。こうして変換式が一旦公式として定まれば、これらを個々のパルス系列に適用することは、機械的な計算となる。熱平衡状態の縦磁化(\(I_{z}\)または\(S_{z}\))から出発して、COSY、NOESY、HSQCといった具体的なパルス系列の場合に、直積演算子がどのように変換されていくのかについても成書を参照されたい。
8. 検知シグナルに含まれる情報
通常NMR装置の信号検知器は、磁化の\(y\)軸に沿った成分を検知するため、変換後最終的に残る\(I_{y}\)成分が、得られるシグナルの特徴を決定する(実際には直交位相検波(quadrature detection)により\(x\)成分と\(y\)成分を同時に検知しているため、より正確には、\(I_{x}+iI_{y}\)を考えなければならないが、以下に述べる結果はほぼ同じである)。
まず1次元スペクトルの場合について考える。
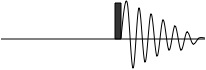
この場合は、平衡状態にある縦磁化に対して、\(x\)軸に沿って90\(^\circ\)パルスをかけ、倒れた磁化が自由歳差運動する過程を、\(y\)軸方向にある検知器で検出するから、直積演算子の展開は
\[I_{z}\buildrel\frac{\pi}{2}I_{x}\over\longrightarrow -I_{y}\buildrel\omega_{I}I_{z}\over\longrightarrow\buildrel 2\pi JI_{z}S_{z}\over\longrightarrow\]
\[\cos\pi Jt(I_{x}\sin\omega_{I}t-I_{y}\cos\omega_{I}t)+\sin\pi Jt(2I_{x}S_{z}\cos\omega_{I}t+2I_{y}S_{z}\sin\omega_{I}t)\tag{67}\]
したがって検知される\(I_{y}\)成分は
\[-\cos\omega_{I}t\cos\pi Jt=-\frac{1}{2}\{\cos(\omega_{I}+\pi J)t+\cos(\omega_{I}-\pi J)t)\}\tag{68}\]
となる(三角関数の公式を用いた)。フーリエ変換後、右辺第1項は周波数\(\omega_{I}\)+\(\pi J\)の位置に,第2項は周波数\(\omega_{I}\)−\(\pi J\)の位置にともに吸収形のシグナルを与える(余弦関数は実フーリエ変換すると吸収形の,正弦関数は分散形の曲線を与える)。また、両項は符号が同じであるから、結果的にスペクトルは、同位相(in-phase)の吸収形シグナルとなる。これは1次元スペクトルの場合、スピン結合によりシグナルが分裂して観測されることに対応する。
次に,2次元COSYスペクトルに関して,検知シグナルの形を見ることにする。
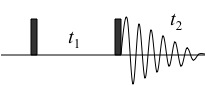
COSYの場合,縦磁化\(I_{z}\)+\(S_{z}\)から出発して最終的には
\[I_{y}\cos\pi Jt_{1}\sin\omega_{I}t_{1}\cos\pi Jt_{2}\sin\omega_{I}t_{2} +I_{y}\sin\pi Jt_{1}\sin\omega_{I}t_{1}\sin\pi Jt_{2}\sin\omega_{I}t_{2}\tag{69}\]
が\(I_{y}\)成分として得られる(\(S_{y}\)成分に関しても同様の項が検知される)。第1項は\(t_{1}\)期と\(t_{2}\)期の周波数が等しいため対角ピークを、第2項は異なるため交差ピークを与える。対角ピークの成分は、
\[\frac{1}{4}\{\sin (\omega_{I}+\pi J)t_{1}+\sin (\omega_{I}-\pi J)t_{1}\}\{\sin (\omega_{I}+\pi J)t_{2}+\sin (\omega_{I}-\pi J)t_{2}\}\tag{70}\]
と変形されるから,これを\(t_{2},\ t_{1}\)方向にフーリエ変換すると、両方向とも\(\omega_{I}\)+\(\pi J\)および\(\omega_{I}\)−\(\pi J\)の位置に、ともに分散形のシグナルを与える。また\(\omega_{I}\)+\(\pi J\)と\(\omega_{I}\)-\(\pi J\)のピークは同符号だから同位相である。同様に交差ピークの成分は、
\[\frac{1}{4}\{\cos (\omega_{S}+\pi J)t_{1}-\cos (\omega_{S}-\pi J)t_{1}\}\{\cos (\omega_{I}+\pi J)t_{2}-\cos (\omega_{I}-\pi J)t_{2}\}\tag{71}\]
となるから,\(t_{1}\)方向には\(\omega_{S}\)+\(\pi J\)および\(\omega_{S}\)−\(\pi J\)の位置に、\(t_{2}\)方向には\(\omega_{I}\)+\(\pi J\)および\(\omega_{I}\)−\(\pi J\)の位置に吸収形のシグナルを与える。また両方とも、\(\omega \)+\(\pi J\)と\(\omega\)−\(\pi J\)のピークの符号が異なるため、反位相のシグナルとなる。
以上のように、COSYスペクトルの対角ピークは同位相の分散形に、交差ピークは反位相の吸収形になる。また三角関数の公式の適用から明らかなように、一般に検知成分の係数が\(\cos\pi Jt\)のとき同位相の、\(\sin\pi Jt\)のとき反位相のシグナルとなる。
このように最終的に観測される直積演算子の成分を調べることにより、得られるピークの位置や形についての情報が得られる。また計算の過程を振り返ることにより、例えば式(69)中のCOSYの交差ピークは、
\[S_{z}\buildrel\frac{\pi}{2}S_{x}\over\longrightarrow -S_{y}\buildrel t_{1}\over\longrightarrow 2I_{z}S_{y}
\buildrel\frac{\pi}{2}(I_{x}+S_{x})\over\longrightarrow -2I_{y}S_{z}\buildrel t_{2}\over\longrightarrow I_{y}\tag{72}\]
のように磁化移動して最終的に検出されることがわかる。
9. コヒーレンス次数(coherence order)
式(57),(58)を導く際に、化学シフトは\(I_{z}\)軸まわりの回転に相当することを述べた。したがって以降では、\(\omega\tau =\phi\)で表し、式(57)、(58)を
\[I_{x}\buildrel\phi_{z}\over\longrightarrow I_{x}\cos\phi +I_{y}\sin\phi\tag{73}\]
\[I_{y}\buildrel\phi_{z}\over\longrightarrow I_{y}\cos\phi -I_{x}\sin\phi\tag{74}\]
と表すことにする。上式と式(38)を用いて、昇降演算子\(I^{+},\ I^{–}\)の\(\phi_{z}\)による変換式を求めると
\[I^{+}\buildrel\phi_{z}\over\longrightarrow\exp(-i\phi )I^{+},\ I^{-}\buildrel\phi_{z}\over\longrightarrow \exp(i\phi )I^{-}\tag{75}\]
多スピン系の場合は同様に
\[I^{+}S^{+}\buildrel\phi_{z}\over\longrightarrow\exp(-2i\phi )I^{+}S^{+},\ I^{+}S^{-}\buildrel\phi_{z}\over\longrightarrow \exp(i0\phi )I^{+}S^{-}\tag{76}\]
のようになる。このように昇降演算子の積では、\(\phi\)による変換により\(\exp(–ip\phi)\)という係数が前に掛かる。またこのとき指数部に現れる\(p\)は、元の演算子中に含まれる各昇降演算子の総和(\(I^{+}\)ならば正に,\(I^{–}\)ならば負に数える)である。この整数\(p\)をコヒーレンス次数(coherence order)と呼ぶ。式(38)を用いることにより、任意の直積演算子のcoherence orderを計算することができる。例えば
\[I_{x}=\frac{I^{+}+I^{-}}{2},\ I_{y}=\frac{I^{+}-I^{-}}{2i}\tag{77}\]
より、\(I_{x},\ I_{y}\)とも、coherence orderが1と–1の項を含む。一方\(I_{z}\)は式(38)により\(I^{+},\ I^{–}\)と結び付けることができず、また
\[I_{z}\buildrel\phi_{z}\over\longrightarrow\exp (i0\phi )I_{z}\tag{78}\]
だからcoherence orderは0である(すなわち縦磁化はcoherence orderに寄与しない)。
一般に、任意の直積演算子を式(77)を用いて昇降演算子の積に変換することにより、coherence orderを計算することができる。このとき、元の直積演算子が\(n\)個の横磁化(\(I_{x}\)または\(I_{y}\))の積であるとき、そのcoherence orderは+\(n\)から–\(n\)まで1つおきにとることができる。例えば、反位相演算子\(2I_{x}S_{z}\)は\(I_{x}\)を1個含むから、coherence orderは+1と–1である。また\(2I_{x}S_{y}\)は横磁化因子を2個含むから、coherence orderは+2, 0, –2である(そしてこの数字が2量子遷移,零量子遷移に対応する)。その理由は以下のようにしてわかる。例えば、\(2I_{x}S_{y}\)の場合,式(77)より
\[2I_{x}S_{y}=2\frac{I^{+}+I^{-}}{2}\frac{S^{+}-S^{-}}{2i}\tag{79}\]
右辺を展開して、昇降演算子の積の和の形にすればよいが、このとき右辺の因数\(\frac{I^{+}+I^{–}}{2}\)から\(I^{+}\)を選べばcoherence orderに+1寄与し、\(I^{–}\)を選べば–1寄与する(\(S\)に関しても同様)。したがって展開後の項のうち、最もcoherence orderが大きいものは、展開時に全て上昇演算子を選んだもので+\(n\)(今の場合には+2)、最も小さいものは、全て下降演算子を選んだもので–\(n\)(今の場合には–2)となる。そしてある選び方に対し、上昇演算子を選ぶ代わりに対応する因数から下降演算子のほうを選ぶと、coherence orderに対する寄与は+1から–1に2だけ下がる(逆の場合は2だけ上がる)から、最終的に得られるcoherence orderは1つおきの値しかとることができない。このように、coherence orderは直積演算子中に含まれる横磁化の数が変わらない限り変化しない。7節で述べた化学シフト、スピン結合による展開ではcoherence orderは変化せず、パルスによって変化することがわかる。こうして各パルス系列に応じ、磁化がどのようなcoherence orderを持って最終的な観測シグナルに伝わるかを表すことができる(これを図示したものをcoherence transfer mapという)。例えば,COSYのパルス系列とcoherence transfer mapは次の通りである。
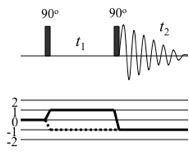
いかなるパルス系列も、平衡磁化から始まり、\(I^{–}\)の状態(\(|\alpha >\)状態から\(|\beta >\)状態への吸収遷移)で観測されるので、coherence orderは0で始まり–1で終わる。
10. 磁化の混合方式
多次元NMRスペクトルでは、あるスピンと別のスピンとの関係(スピン結合やNOE等)をスペクトル上の交差ピークとして表示するため、測定においては、あるスピンの磁化情報を他のスピンへどのように伝えるか(これを磁化の混合(mixing)という)が重要となる。また、これらの混合技術を組合わせることにより、(特に3次元以上では)スピンに関する選択的な情報を抽出することが可能となる。以下では、代表的な分光法で用いられる磁化の混合方式を、直積演算子の概念を用いて解説する。
10.1 COSY
COSYの磁化移動は、第2の90°パルス(混合パルス)に負っている。式(72)に示した通り、まず第1の90°パルス(励起パルス)により横磁化が発生する。横磁化は\(t_{1}\)期の展開中に、7節で述べように、反位相磁化を形成する(これはスピン結合による展開のためである)。そしてこの反位相磁化が混合パルスによって分極移動(polarization transfer)を起こし、式(66)のように相手側のスピンの反位相磁化となる。
相手側スピンに移った磁化は、この後の\(t_{2}\)期の展開により、再び(同位相の)横磁化となって観測されることになる。「反位相磁化の形成と混合パルスによる分極移動」が磁化移動の骨子である。なお、8節で見たように、COSYにおいては対角ピークが分散形となり、裾を引いてスペクトルの重なりが激しくなる。このため、2量子フィルターを用いて観測することが多い(DQF-COSY)。
10.2 NOESY
1節で述べたように、NOESYのパルス系列は、第2のパルスまではCOSYと全く同様である。
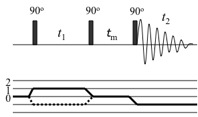
したがって第2のパルスをかけた後に存在する全直積演算子は、COSYの場合と同じである。このうちCOSYでは反位相演算子の項(式(69))が観測の対象となったが、NOESYでは縦磁化成分 \[-I_{z}\cos\omega_{I}t_{1}\cos\pi Jt_{1}\tag{80}\] がその後の観測の対象となる(\(S_{z}\)成分も同様)。この後の混合時間(第2パルスと第3パルスの間)に、交差緩和により、スピン\(I\)とスピン\(S\)の磁化成分が一部交換される(この機構は直積演算子よりも古典的な緩和機構で考えたほうがわかりやすい)。 \[-(I_{z}a_{II}+S_{z}a_{IS})\cos\omega_{I}t_{1}\cos\pi Jt_{1}\tag{81}\] そして第3の90\(^{\circ}\)パルスにより、これら縦磁化が横磁化に変換され \[I_{y}a_{II}\cos\omega_{I}t_{1}\cos\pi Jt_{1}+S_{y}a_{IS}\cos\omega_{I}t_{1}\cos\pi Jt_{1}\tag{82}\] \(t_{2}\)期の展開で観測されることになる。このうち上式第1項は混合時間中に磁化の交換がなかった項で対角ピークに、第2項はスピン\(I\)からスピン\(S\)に磁化移動があった項で交差ピークに対応する。以上のようにNOESYでは、「混合時間における縦磁化同士の交差緩和による磁化交換」が磁化移動の骨子である。なおこのときの磁化移動の効率(上式の\(a_{IS}\))は,混合時間に依存し、その初期勾配が交差緩和速度\(\sigma_{IS}\)として、2原子間の距離を与えることになる。
10.3 INEPT
異種核間スピン結合の情報伝達方式として、まずINEPTを取り上げる。INEPTのパルス系列の基本は、90\(^{\circ}\)パルス(\(I\))→\(\Delta\)→180\(^{\circ}\)パルス(\(I,\ S\))→\(\Delta\)である。
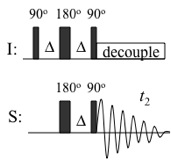
\(I\)は\(^{1}\)H,\(S\)は他核(\(^{15}\)N,\(^{13}\)C等)を表す。このパルス系列により、反位相磁化\(2I_{x}S_{z}\)が形成する過程は、古典的磁化ベクトルモデルによっても説明可能である。ただしここでは次のように理解することにする。
まず展開時間の真ん中で180\(^{\circ}\)パルス(refocusing pulseという)を打つと、
(i) 一方の核種のみにかけた場合、化学シフトと異種核間スピン結合による展開が、結果的に抑えられる。
(ii) 両方の核種に同時にかけた場合、化学シフトによる展開が、結果的に抑えられる。
理由は、磁化ベクトルモデルからも直積演算子の変換式からも説明できる。
したがってINEPTの場合は(ii)に相当するから、最初の90\(^{\circ}\)パルスにより発生した横磁化\(-I_{y}\)が、実質2\(\Delta\)の時間中にスピン結合のみの展開を受けることになり、
\[I_{y}\buildrel2\pi JI_{z}S_{z}\over\longrightarrow -I_{y}\cos\pi J2\Delta + 2I_{x}S_{z}\sin\pi J2\Delta\tag{83}\]
このスピン結合には、同種核間、異種核間ともに存在するが、前者は後者に比べて小さいため、後者のみ考えればよい。いま\(\Delta = \frac{1}{4J}\)とすれば、上式右辺の第2項のみが残り、上述のように反位相磁化\(2I_{x}S_{z}\)が形成される。INEPTでは、このあと90\(^{\circ}\)パルスにより、スピン\(S\)の反位相磁化に分極移動させ、最終的に(スピン\(S\)の)同位相の横磁化として観測する。
10.4 HSQC
INEPTでは、異種核間スピン結合の情報を、最終的にスピン\(S\)(励起核とは異なる核種)で検出したが、これを再度INEPT型の磁化移動により元のスピン\(I\)に戻して観測するのが、HSQCである(理由は最終的なシグナル感度のためである)。
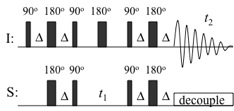
戻す前に\(t_{1}\)期を設けてスピン\(S\)の化学シフトで展開させれば、\(t_{1}\)方向の周波数は\(\omega_{S}\)となり,\(t_{2}\)方向(すなわち検出期)の周波数\(\omega_{I}\)とともに2次元上の交差ピークとなる。また\(t_{1}\)期の真ん中に、異種核間スピン結合およびスピン\(I\)の化学シフトによる展開を抑えるため、180\(^{\circ}\)パルスをスピン\(I\)のみにかける(上記の(i)の場合に相当する)。このようにHSQCは、磁化移動の観点から「INEPT→\(t_{1}\)→reverse INEPT→\(t_{2}\)」として説明することができる。
10.5 その他
以上の磁化移動の技法を組み合わせれば、種々の3次元3重共鳴測定をデザインすることが可能である。例えばHNCOの実験は、「まず\(^{1}\)Hを励起し、INEPTにより\(^{15}\)Nに磁化移動する。\(^{15}\)Nで\(t_{1}\)期に展開した後、生成した(カルボニル基の\(^{13}\)Cに関する)反位相磁化を90\(^{\circ}\)パルスにより分極移動させ、\(t_{2}\)期に展開させる。あとは逆の手順で磁化を戻し、最終的に\(^{1}\)Hで\(t_{3}\)期に検出する」と読むことができる。このとき、不必要な核種の化学シフトやスピン結合による展開を抑えるため、適宜refocusing pulseをかけることになる。
11. おわりに
以上のように直積演算子の概念を用いれば、種々の多次元NMRの測定技術の理解が容易となる。なお本ページにおいて、緩和の影響については考慮していないので注意されたい。以上興味ある方の参考になれば幸いである。